1. 前言

在打工的时候，接触到FFT相关的内容，因此上网恶补了一下，感慨自己以前信号与系统和DSP学得不太好。
然后看到一篇Report文章：Spectrum and spectral density estimation by the Discrete Fourier transform (DFT), including a comprehensive list of window functions and some new flat-top windows.
https://holometer.fnal.gov/GH_FFT.pdf
把这篇文章翻译了一下，并且添加了一些自己的理解。有兴趣可以点进去看原文。

傅里叶变换这个东西可以说非常熟悉又有点陌生。经常我们在解决一些问题的时候会用到傅里叶变换。
对数字信号来说，“Fourier Transform”即“Discrete Fourier Transform, DFT”，而计算用DFT用的方法一般都是“快速傅里叶变换，FFT”。那么接下来就按照我看的一篇英文的Report，理一下对一个时域数字信号进行离散傅里叶变换，要做多少额外的工作。（虽然FFT不等同于DFT，现实中计算DFT通常用的就是FFT算法，所以下文就把DFT和FFT看成一个意思）

那进行DFT主要是为了求得信号的频谱/频谱密度。
在工程和实验上，应用最广泛的是“优化后重叠、分段且平均的周期图Overlapped segmented averaging of modified periodograms”。(渣翻译)
周期图(periodogram)意思是对时域的一个片段进行DFT，修改后的(modified)意思是对时域信号加窗、平均化，用于减小计算得到的频谱的波动。这个方法由“welch”提出，并且被熟知于一些关键词像“WOSA” (Welch’s overlapped segmented average)等等。
那么，从Section 2 到 Section 11，讨论各种独立的问题，如尺度、加窗、平均。在Section 12中总结这些工作。两个更专业的话题在原文的附录A和B中讨论（A：实信号的最大动态范围，B：如何计算window function的频率响应）原文的附录C和D在细节上描述一些常见和有用的窗函数，包括原文其中一位作者(G.H.)开发的高性能窗函数(flat-top window function)。

补充：频谱与频谱密度

(频谱和频谱密度傻傻分不清)

频谱 Spectrum
频谱密度 Spectral Density

频谱和频谱密度有“Power”功率和“Linear”线性两种，即：
Power Spectrum
Power Spectral Density
Linear Spectrum
Linear Spectral Density
其中，Linear对Power的关系是Linear Spectrum/Spectral Density是Power Spectrum/Spectral Density的开根号：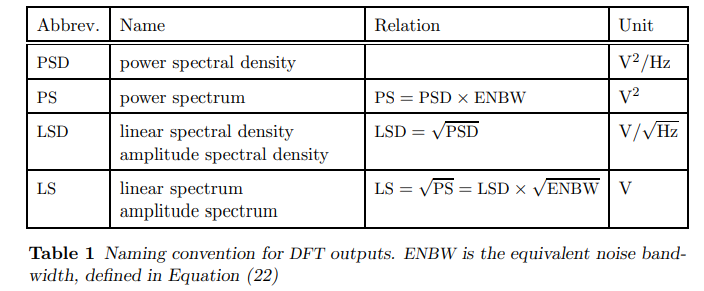

在电子上，通常“功率”与电压值的平方成正比（由欧姆定律$P=U^2/R$，这里常数R不变），所以“Power”的单位是带平方的，而“Linear”的单位不带平方。

那 Spectrum 和 Spectral Densitys 之间的关系呢？上面的式子展现了PS是PSD与ENBW的乘积，ENBW, effective noise bandwidth, 有效噪声带宽，这在Section 8: window function继续讨论。
The effective noise bandwidth ENBW is given by: $$ ENBW = NENBW\cdot f_{res} = NENBW \cdot \frac{f_s}{N} = f_s \frac{S_2}{(S_1)^2} $$ 先不看这个与“window function”有关的“有效噪声带宽”。“功率谱密度(Power Spectral Density)”描述的是时域信号的【能量】随着频率的分布情况。数学上，是时域上【自相关】序列的傅里叶变换。也就是说，我们对一个自相关的时域序列做DTFT，得到的就是“Power Spectral Density”。
时域$x(t)$中离散信号的功率谱密度$S(f)$为：
$$ S(f) = \frac{1}{N} \left | \sum_{n=1}^{N} x_n(t=n \Delta t)e^{-i2\pi fn\Delta t} \Delta t \right | ^2 $$ 这里，Power spectral Density仅仅是信号的傅里叶变换。如果时域信号x(t)有N个样本，n表示样本数，离散的情况下，为了满足因果信号，积分下限从t=0开始。从“Weiner-Khinchin theorem”知道，这个自相关的时间序列x(t)和它的Power Spectral Density是傅里叶变换对。
注意：由于DFT的周期化处理，DFT得到的是频谱，DTFT得到的是频谱密度。
那Power Spectrum是什么呢，我们考虑有限频段内的总信号含量，这个量被称为“带限功率谱”，简称“功率谱”。对于给定的功率谱密度$S(w)$，带限功率谱为：
$$ \frac{1}{\pi} \int_{\omega_1}^{\omega_2}S(\omega)d\omega $$ 也就是Power Spectrum是Power Spectral Density在一定频带范围内的定积分。这与概率论的“概率分布”和“概率密度”有相似之处，概率分布为概率密度的积分。
Power Spectrum的单位是$V^2$，而Power Spectral Density的单位是$V^2/Hz$。这个$V^2/Hz$表示【时域电平的方差】，这恰好与频域中给定信号的电功率含量成比例。
这个“带限”可以理解为一个frequency bin里面的下界和上界之间。来看这样一张图：

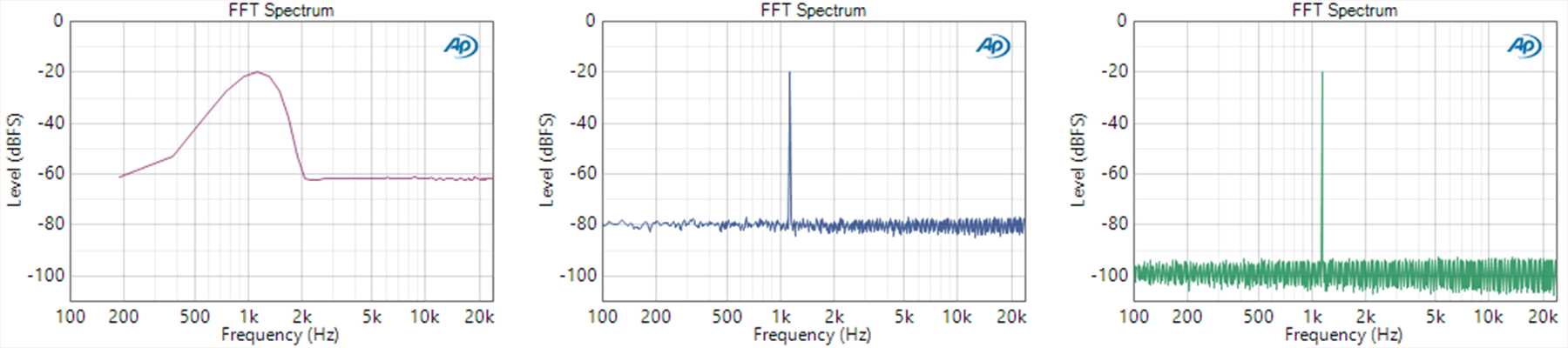
对于Spectrum，同样一个信号，随着FFT点数的增加，noise floor会下降。这是因为FFT点数N增加，frequency bin的积分区间就会减小，因此对Spectral Density的积分结果就减小了，同样一个信号，noise floor应该是一样的，但是FFT的点数增加，Spectrum显示的noise floor就下降了。但是对于中心频点，frequency bin的增加和减小并不会太影响信号自己的Spectral Density的积分结果，因为noise足够小。

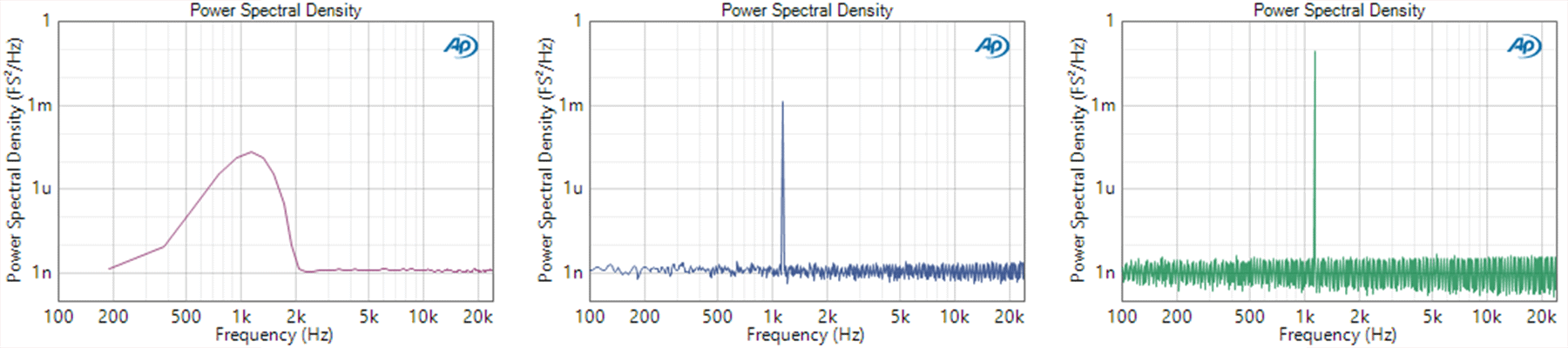
而对于Spectral Density，随着FFT点数增加，frequency bin减小，信号的noise floor就不变了，但是中心频点的电平随着frequency bin的减小而增大。可以理解为，用一个个小的”带限滤波器“去滤该信号的每一个频率来看信号在该频率下的功率。如果frequency bin减小，这个”带限滤波器“更精确地落在细微的频率上，所以对于某个特定的频率选择性更好，因此这个peak看起来会变得更窄、更高（也可以从delta函数的角度理解，如果信号的积分不变，时域范围收窄，那么信号的尖峰会更高，这里delta的”积分“相当于能量）。对于noise floor, 因为没有对一定频率范围内的噪声功率做积分，所以noise floor不会提升或者下降。
这样，Spectral Density可以用于观测noise floor的水平，与FFT的点数N无关，而Spectrum可以用于观测某一中心频率的level，与FFT的点数N无关，但是需要选择合适的window 如 “flat-top window”（在Section 8中讨论）

2. 介绍

举个例子，我们考虑一个频率为1234Hz，振幅为2$V_{rms}$的正弦信号$x(t)$。此外它含有功率谱密度为10m$V_{rms}/Hz$的噪声，带宽范围从50Hz到2000Hz。这个信号的Spectrum 如 Figure 1 所示，虽然y轴没有标定（因为同一张图有两种单位）。
然后我们假设这个信号被ADC以固定的采样频率fs=10kHz采样。
我们想要如Figure 1那样能让我们直观地检测到peak的振幅（2Vrms）以及noise floor（10m$V_{rms}/\sqrt{Hz}$）的等级。我们已经注意到这两个单位是不一样的，因此需要对y轴进行不同的度量(scale，不知道怎么翻译好)。因此我们想要两张图，一个以V为尺度，另一个以$V/\sqrt{Hz}$为尺度。前者是"(Linear) Spectrum", 后者是"(Linear) Spectral Density"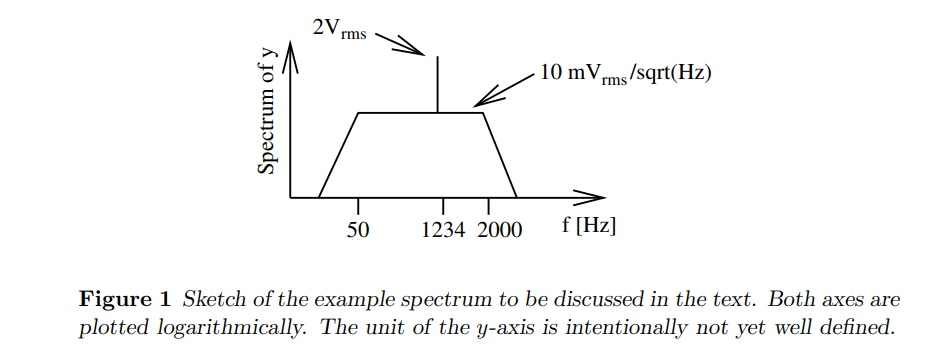

这个功率谱密度(Power Spectral Density)描述时域信号能量随着频率的分布情况，详细的如上面补充部分所述。
这个 Linear spectral density 是 Power spectral density的均方根，Linear Spectrum 与 Power Spectrum同理。对于Linear spectral density，经常使用$V/\sqrt{Hz}$这个单位。通常用一个tilde(~)在符号的顶上来表明它，例如，一个连续电压 $U_{something}(t)$ 相应的Linear Spectral Density 用 $\widetilde{U}_{something}(f)$ 来表示。 Linear Spectral Density $\widetilde{U}(f)$ 一个几乎重要的关系 是电压值 U 与他的rms波动之间的关系，假设它被带限在频率范围 $f_1$ 到 $f_2$ 之间：

$$ U_{rms} = \sqrt{\int_{f_1}^{f_2}\left [ \widetilde{U}(f) \right ]^2 df } $$

（补充，就是Spectrum是Spectral Density的积分，这式子里面的”根号“和”平方“是因为里面的是Linear的U而不是Power）
表1总结了4种不同的方法来表示DFT的结果，假设输入的时域信号用Volts来表示。

实验者通常更喜欢”Linear“的版本，因为这可以直接与实验的参数相关（不用转换）。
Spectrum和Spectral density之间的关系，由Effective Noise Bandwidth（有效噪声带宽，ENBW）给出，并且可以在DFT计算出来的时候被简单地决定。但是，Spectrum和Spectral density之间不可以直接互换，在没有额外条件的情况下。

3. 电压的尺度(scale)

外面连续的电压信号进入ADC，而我们从ADC输出得到的已经是量化成二进制bits的离散数字信号。在进入我们的计算之前，先从【ADC量化的整数】转化成【电压浮点数】，这非常简单，乘上一个因子就可以了： $$ U_{LSB}=\frac{U_{max}-U_{min}}{2^n} $$ 这里$U_{LSB}$是电压对应的最低有效位，n对应ADC的位数。
注意： $U_{max}$和$U_{min}$并不是外部限制of输入电压的范围，只是最高和最低的电压分辨率的两个通常的点。
补充： 这里很好理解，假如外面输入的电压范围是-10V到10V，ADC量化精度8bits，那么一个bit对应的电压范围就是0.078125。假如现在从ADC得到的数据是“-6”，就用“-6”乘这个$U_{LSB}$，这个ADC输出的量化过的数字对应实际电压就是0.46875V。当然实际的信号处理过程一般不注意实际电压，而是“归一化电压”，让输入电压的范围在-1V到1V之间，这样“0dBFS”对应的就是±1V，实际对应外面的电压就是±10V了。

4. Discrete Fourier Transform

离散傅里叶变换通常是一个长度为N的复向量：$x_k$, k=0,…, N-1, 转换到一个长度为N的复向量：$y_m$，m=0,…,N-1 的变换。
这里DFT有三个不同的定义，它们之间的区分仅仅在于不同的归一化因子：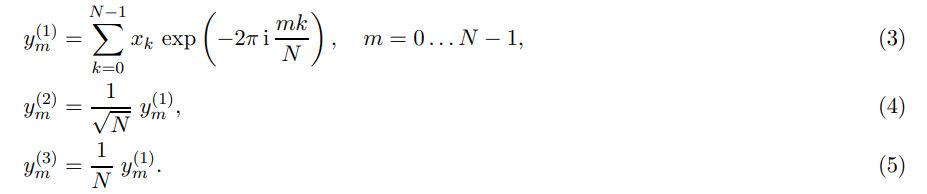

这个变换叫做“Forward DFT”，有前向自然有反向，反向“Backword DFT”与前向的区别是exp的符号：反向是 $+2\pi i \frac{mk}{N}$，而前向是 $-2\pi i \frac{mk}{N}$
在电脑上实现DFT，通常使用FFT算法。不同的软件包可能用上面三种不同的计算方法。大多数FFT package（例如FFTW），计算的是$y(1)$。
而Fourier function of Mathematica（注：Mathematia是一个常用的数学分析数学分析软件）计算$y(2)$，顺带一提，这是唯一一个以对称的方式来定义前向DFT和后向DFT，这样可以依次应用前向和反向DFT来重现原始数据。
最简单的计算spectrum 的方法，是$y(3)$。如果我们再次考虑正弦信号的话，这可以被直接看到。如果我们增加N，$y(1)$将会提取越来越多的信号，并且在适当的frequency bin下，结果会正比于N增加，然而我们想要的结果，amplitude，显然易见地并不取决于N。
如果是通常情况做DFT，一般会使用window functions，这个窗有关的归一化会处理这个因素(见Section 9)。尽管如此，当第一次使用一个FFT算法，注意选择实际计算上述三个式子中的哪一个式子。

虽然在一般的DFT定义中，$x_k$是复数，不过时域数字信号一般是实数。因此，这个输出数组$y_m$遵守以下关系： $$ y_{N-m}=y_{m}^* $$ (*)符号表示复共轭。实际上，如果N是偶数，$y_0$和$y_{N/2}$就是实数。从现在起我们假设N是偶数。因此数组的后半部分，$y_{N/2+1}…y_{N-1}$ 是多余的，有些FFT package不会计算它们。这个结果被典型地返回在一些packed的格式里面。例如FFTW package，这个结果是一个实向量$z_i$，i=0…N-1 : $$ z_{i} = \Re(y_i), 0\leq i \leq N/2, $$ $$ z_{N-i} = \Im(y_i), 0\leq i \leq N/2 $$ (注释：上面是实数部分，下面表示虚数部分，意思是实部和虚部拼接成为一个一维数组，并且对称）
如果只有【复数到复数】的FFT算法是能用的，在Section12.3 中参考 Press 描述了两个方法，用一般的效率来计算实数到复数傅里叶变换。

因为上面的关系，通常为了方便，把N设置为偶数，后面我们都假设N是偶数。有一些程序甚至要求N是2的power（幂）。然而，有些情况限制没有那么严格。例如FFTW package，可以用任何正整数N计算DFT，并且对于这个形式的整数有高的效率：
$$ N=2^a3^b5^c7^d11^e13^f $$ $e+f$是0或者1，其他指数随意。这样在选择频率分辨率$f_{res}$时给了更多灵活。

本段小结：

1. 进行DFT注意一下选择的“归一化因子”是什么。
2. 对于实信号到复信号的DFT，后半部分于前半部分共轭对称，因此实际应用中后半部分可以忽略。
3. 对于某些FFT程序，N需要是2的幂。退而求其次，DFT长度N最好是偶数。

(未完待续)

Reference:

https://holometer.fnal.gov/GH_FFT.pdf
Spectrum and spectral density estimation by the Discrete Fourier transform (DFT), including a comprehensive list of window functions and some new flat-top windows.

https://www.ap.com/blog/fft-spectrum-and-spectral-densities-same-data-different-scaling/
FFT Spectrum and Spectral Densities – Same Data, Different Scaling- AP

https://resources.pcb.cadence.com/blog/2020-power-spectrum-vs-power-spectral-density-what-are-you-measuring
Power Spectrum vs. Power Spectral Density: What Are You Measuring? - Cadence